Historic Victory at the World’s Premier Theorem Proving Competition
The CADE ATP System Competition (CASC) is the annual world championship for fully automatic, classical logic automated theorem proving (ATP) systems. It publicly evaluates and compares the capabilities of ATP systems, encourages research and development, and promotes robust, deployable tools for real-world applications. CASC also fosters interaction among ATP researchers and raises awareness of ATP technology beyond the research community. Systems are assessed by the number of problems they solve within defined time limits, the quality of their solutions, and their average solving time. The competition is chaired by an independent panel of expert researchers.
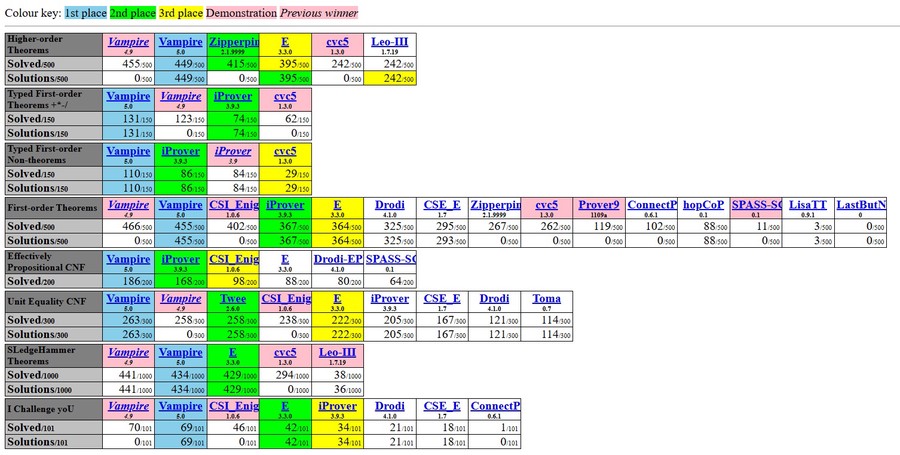
The Vampire theorem prover has made history at the annual CASC-30 by winning all eight theorem‑proving divisions. This marks the first time in CASC history that a single prover has achieved a complete sweep. Even more impressively, Vampire solved more problems than all other competing systems combined.
Automated reasoning is now a cornerstone of verifying the correctness of modern software systems and services — from Boolean satisfiability (SAT) and satisfiability modulo theories (SMT) to automated theorem proving in first‑order and higher‑order logic. Vampire has evolved into one of the most advanced ATP systems available, excelling in saturation‑based theorem proving for practical applications such as software certification, security analysis, and the automation of mathematics.
The diary of improvements in Vampire since the 2013 tutorial paper by Laura Kovács and Andrei Voronkov was presented at the flagship International Conference on Computer Aided Verification (CAV 2025), where the work was honored with the Distinguished Paper Award.
The paper’s authors are:
- Filip Bártek (Czech Technical University in Prague),
- Ahmed Bhayat (University of Manchester),
- Robin Coutelier (TU Wien),
- Márton Hajdu (TU Wien),
- Matthias Hetzenberger (TU Wien),
- Petra Hozzová (Czech Technical University in Prague),
- Laura Kovács (TU Wien),
- Jakob Rath (TU Wien),
- Michael Rawson (University of Southampton),
- Giles Reger (University of Manchester),
- Martin Suda (Czech Technical University in Prague),
- Johannes Schoisswohl (TU Wien),
- Andrei Voronkov (University of Manchester / EasyChair).
The latest developments in Vampire include:
-
Advanced logical reasoning in polymorphic first‑order logic with theories, induction, and quantifiers.
-
Integration of SAT solving with first‑order theorem proving via the AVATAR framework.
-
Native quantified reasoning with mixed arithmetic, enhanced by superposition and quantifier elimination.
-
Second‑order induction schemata embedded as inference rules in proof search.
-
Full support for higher‑order logic, program synthesis, and counterexample generation.
These advances allow Vampire to outperform or complement state‑of‑the‑art reasoners, including leading SMT solvers and inductive theorem provers. Its unmatched performance at CASC‑J12 demonstrates its ability to consistently prove more problems than any other system across every competition division.
With a decade of continuous development, a new permissive license, and unprecedented reasoning power, Vampire stands as a key tool for advancing formal verification, logic program validation, system security, and the automation of complex mathematical reasoning.
© Daniela Jung © TPTP World